Греческая математика

Речь пойдет об узкой части греческой математики, об обозначении чисел.

Буквенная нумерация

Греки обозначали цифры буквами алфавита. Буквенная нумерация - не греческий эксклюзив: греки позаимствовали её примерно в III в. до н.э. у финикиян (Юшкевич, хотя Томас Хит относит первое упоминание примерно к 450 г. до н.э.), а потом её повсеместно использовали и славяне, и евреи, и сирийцы, и арабы (т.н. арабские цифры - гораздо более позднее изобретение), и грузины, и армяне. У греков это обозначение называется ионийским, а до него использовалось аттическое / беотийское (по областям балканской Греции, где существовали мелкие отличия) или геродианово (по имени грамматика Геродиана, который описал её во II в. н.э.). Я не буду касаться геродиановых обозначений, потому что до античности они не дожили, а нам интересно, что там у Птолемея.

Целые

Греки использовали следующие буквенные обозначения:

Буквенные обозначения чисел
ноль		единицы		десятки		сотни
ноль		буква	число	буква	число	буква	число
○ (НЕ ноль, а кружок)	0
		α	1	ι	10	ρ	100
		β	2	κ	20	σ	200
		γ	3	λ	30	τ	300
		δ	4	μ	40	υ	400
		ε	5	ν	50	φ	500
		ς (стигма) или ϝ (дигамма)	6	ξ	60	χ	600
		ζ	7	ο	70	ψ	700
		η	8	π	80	ω	800
		θ	9	ϙ (коппа)	90	ϡ (сампи)	900

Немножко прокомментирую приведенный список цифробукв.

○ - это не ноль, а кружок. 0 как число появилось все-таки в Индии. Но 0 как цифра, как знак, указывающий на отсутствие целой части числа появился у греков в виде ○. Возможно, это наследие счета на греческом абаке, счетах с камешками, где в качестве пустого разряда использовался круглый камешек с дыркой, называвшийся ψηφος (что и означает "камешек").

Классический алфавит античных греков включал 24 буквы, и поскольку их не хватало на полноценное обозначение чисел до 1000 (а нужно 9 x 3 = 27), греческие математики добавили три архаичные буквы, вышедшие из употребления еще в IV в. до н.э., до формирования нумерации: дигамму, коппу и сампи.

Дигамма ("двойная гамма", она же, в раннем варианте, вау / вав от исходной финикийской буквы) ϝ звучала как звонкое w. Стигма ς - это поздний византийский курсивный вариант дигаммы. Зачем он был нужен в поздневизантийкий период (после 1000 годов), если исходная дигамма к тому времени уже полтора тысячелетия не существовала, я не понимаю. Стигма очень похожа на концевую сигму σ -> ς (сигма в конце слова в современном греческом), но формально это разные буквы. Формально же, стигма - это лигатура σ + τ. Ну и наконец, я не знаю этимологической связи между "стигмой" и "стигматами".

Коппа ϙ - это глухой "к", от которого растет латинское q. Позднее начертание коппы, применяемое и в юникоде, похоже на молнию - Ϟ (в некоторых кодировках отображается "обычной" коппой), но для чисел оно не используется.

И последняя дополнительная буква греческой арифметики, сампи ϡ. Звучала, вероятно, как [с], вытеснена сигмой.

Вернемся однако ж к математике.

На 999 алфавит исчерпывался, и чтобы считать тысячи, использовались те же знаки, что и для первого десятка от α до θ, но перед ними слева внизу ставился штрих, примерно так: _\α = 1000. Больше 9000 у греков запала, однако, не хватило (и полноценного позиционного обозначения они, увы, не открыли), и 10.000 обозначается не _\ι, а специальным символом M. Дальнейшие подробности больших чисел я опускаю, потому что они на практике встречались редко.

Чтобы отличить на письме числа от текста, над ними или ставилась черта: 123 = ρκγ, или они закрывались верхней засечкой: 456 = υνς^/.

Таким образом греки обозначали целые числа.

Дроби

Долгое время греки не считали дроби числами, а воспринимали их как действия над целыми, как операции с частями целого числа. Четвертая (часть) -> 4-ая -> δ^ων, третья (часть) -> 3-я -> γος: греки поступали в математических текстах точно так, как поступаем сейчас мы на письме, прибавляя к числу-основанию грамматический суффикс в надстрочном регистре. Для сокращения суффикс постепенно заменился штрихом или двойным штрихом: 1/4 = δ' или 1/3 = γ". Были и другие варианты надстрочных символов.

Две трети могли написать так: β γ^ος или так: β γ'. Но такое обозначение несло двузначность понимания, ведь это же выражение - β γ' - можно было прочитать и как 2 1/3! Понять значение можно было только из контекста, вникая в математический смысл текста.

По этой или по иной причине, примерно во втором веке до нашей эры пришли к греки знакомой нам записи дроби в виде числителя и знаменателя друг над другом. Правда, они располагали их обратным образом, знаменатель наверху, числитель внизу:

 1 3/4 = α ^δ_γ.

Позже в обиход начало входить знакомое нам обозначение, называвшееся "индийским", числитель наверху, знаменатель внизу. Отсюда пошли наши обыкновенные дроби:

 1 3/4 = α ^γ_δ.

Это было вполне удобное обозначение натуральных дробей. Но греки использовали и другие способы.

Аликвотные дроби

Александр Македонский завоевал Египет в 30-х годах IV в. до н.э. и основал в 332 году Александрию, ставшую новым центром эллинистической культуры. К этому времени египетская математика безнадежно отстала от греческой, но тесное взаимодействие традиций оказывало влияние. В частности, греки начали применять египетские дроби.

Египтяне использовали так называемые аликвотные дроби, или основные, или единичные - это дроби с числителем единица: 1/2, 1/3, 1/4 и т.д. Чтобы в счете получить иные дроби, необходимо суммировать несколько основных: 3/4 = 1/2 + 1/4, 8/15 = 1/3 + 1/5, 2/43 = 1/42 + 1/86 + 1/129 + 1/301.

В арифметических расчетах египетские дроби крайне неудобны, хотя, конечно, математики придумали способы и приемы облегчить себе жизнь (Ван дер Варден даже считает, что это стало одним из ограничителей развития египетской математики; мне, однако, представляется, что если бы необходимость в том была, были бы проведены соответствующие нормативные реформы), но в качестве константных значений египетские дроби можно было использовать. Так, в звездном каталоге "Альмагеста" (137 г.) Птолемей применял египетские аликвотные дроби ~~и ничего не боялся~~; по всей видимости, египетские дроби были и в каталоге Гиппарха(139 г. до н.э.).

Греки взяли идею аликвотных дробей у египтян, но использовали, конечно, свои родные буквенные обозначения. Основная дробь обозначалась штрихом:

 1/2 -> β'
 1/3 -> γ'
 1/4 -> δ'

и т.д.

Сумма аликвотных дробей, формировавшая произвольную дробь, выглядела так:

 3/4 = 1/2 + 1/4 -> β' δ' (или так: β' δ^x)
 8/15 = 1/3 + 1/5 -> γ' ε'
 2/43 = 1/42 + 1/86 + 1/129 + 1/301 -> μβ' πς' ρκθ'

Наконец, целая с дробью представлялась греками следующим образом:

 1 3/4 = 1 + 1/2 + 1/4 -> α β' δ'.

Для двух часто употребимых дробей у греков были специальные обозначения:

1/2 -> 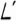, L' (происхождение неясно) или Ϲ' / Ͻ' (это просто половинки беотийского обозначения единицы ○, в свою очередь, образовавшегося от слова "обол" [Томас Хит]; в Беотии кружок = единица!)
3/4 -> 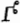Именно этот крючочек заинтересовал меня при изучении "Альмагеста" и побудил изучить вопрос греческих обозначений чисел подробнее, но происхождение его так и осталось не ясно. Это похоже на лигатуру Γ^β, восходящую к обыкновенным дробям в "индийском" написании, но я не нашел этому подтверждения.

Египтяне иногда употребляли специальный иероглиф для 3/4, но подобное греческое употребление мне не встречалось.

Шестидесятеричные дроби

Птолемей подтверждал, что использовать в расчетах греческие дроби неудобно. Для расчетов они и не использовались, у греков было мощное продвинутое средство: шестидесятеричные дроби.

Шестидесятеричная система счисления была придумана шумерами еще в III тысячелетии до нашей эры и унаследована вавилонянами. Не буду отвлекаться на её ближневосточную историю, а перейду сразу к грекам: греки, я полагаю, познакомились с этой системой примерно в VII веке до н.э., с налаживаем культурных контактов со Междуречьем. Однако, применяли они её только в приложении к дробям.

Вавилонская система эквивалентна нашей десятеричной системе, только в её основании лежит на десять, а шестьдесят. Шестидесятеричные дроби вполне ясны, это дроби с основанием 60:

 1/60,
 1/60² = 1/3600,
 1/60³ = 1/216000

и т.д.

Понятно и их использование, вот корень из трех (это конкретный пример из Птолемея):

 √3 = 1 + 43/60 + 55/60² + 23/60³ -> α μγ' ηε" κγ‴ .

Обратите внимание на два факта.

Во-первых, оперировать с шестидесятеричными дробями было исключительно просто, не сложнее, чем с десятичными. Птолемей, по словам Ван вар Вардена, обходится с ними виртуозно, нигде, правда, не описывая конкретную технику. Однако античные комментаторы подробно объясняют эти приемы.

Во-вторых, большое основание вавилонских дробей позволяет компактно записывать дробные числа, так, приведенное значение корня из трех, включающее три дроби, верно до седьмого знака после запятой в современной десятичной записи.

Кстати, о запятых.

Историки математики воспроизводят вавилонские дроби, удобства ради отделяя целую часть точкой с запятой и шестидесятеричные дроби запятыми, вот так:

 √3 = 1 + 43/60 + 55/602 + 23/603 = 1; 43, 55, 23.

Ну и наконец, заметьте: вавилонские дроби в греческой записи точно эквивалентны современному обозначению углов, географических координат и времени! Вот, например, координаты Москвы (широта и долгота) в современном и древнегреческом обозначении:

 55° 45' 21" -> νε με' κα",
 37° 37' 04" -> λζ λζ' δ".

Резюме

Для обозначения целых чисел греки использовали десятичные непозиционные буквенные обозначения.
Для обозначения дробей греки использовали три способа:
- обыкновенные дроби, помещая числитель под знаменателем,
- египетские аликвотные дроби, отмечая их штрихом, обычно для константных величин,
- вавилонские шестидесятеричные дроби, отмечая их штрихами соответственно разряду, для вычислений.

Источники

Б. Л. ван дер Варден, "Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции".
"Истрия математики с древнейших времен до начала XIX столетия" в трех томах под редакцией А.П. Юшкевича.
"Истрия греческой математики" сэра Томаса Хита.
Э. Кольман "История математики в древности"